“欲穷千里目, 更上一层楼” 是唐朝诗人王之涣在《登鹳雀楼》中的名句, 那现在的问题是上一层楼能否穷千里? 若否, 需多高?
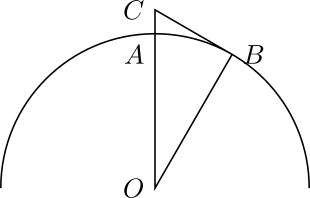
如图, 地球几乎是球体, 若在 $A$ 点有一栋楼, 高到点 $C$ 才能看见千里外的点 $B$, 也就是劣弧 $\wideparen{AB}$ 的长度为 $1000$ 里 $=500\,\mathrm{km}$, 地球的半径取 $6370\,\mathrm{km}$. 则 $\angle AOB=\frac{500}{6370}\,\mathrm{rad}=\frac{50}{637}\,\mathrm{rad}$, 利用一点三角函数可得
\[AC=\frac1{\cos\frac{50}{637}}\times6370-6370\approx19.67\,(\mathrm{km}).\]
这样看来只上一层楼还是不行了. 不仅如此, 目前世界上还没有这么高的楼, 最高的也就一千多米而已.
这个方法计算需要一般的三角函数值, 一般没法直接计算, 考虑到 $\angle AOB$ 太小, 可以近似计算. 由于 $\frac{500}{6370}\approx\frac1{12.8}$, 则 $CB\approx\wideparen{AB}=500$, 根据勾股定理可计算得
\begin{equation}AC=\sqrt{6370^2+500^2}-6370\approx19.59\,(\mathrm{km})\label{eq:app1}.\end{equation}
当然了当前会手算开平方的能有几人, 那把式 \ref{eq:app1} 分子有理化后近似计算可得下式.
\[AC=\sqrt{6370^2+500^2}-6370=\frac{6370^2+500^2-6370^2}{\sqrt{6370^2+500^2}+6370}\approx\frac{500^2}{2\times6370}\approx19.62\,(km).\]
在第一种中, 直接用 $\sqrt{1-\frac{50^2}{637^2}} \approx \sqrt{1-\sin^2\frac{50}{637}}$ 换掉 $\cos\frac{50}{637}$ 可得类似结果.
另外借助于 $\alpha\approx0\Rightarrow \tan\alpha\approx\alpha$, 由 $\angle ABC=\frac12\angle AOB$ 可近似得到 ($\angle BAC\approx\frac{\pi}2\,(\mathrm{rad})$)
\[\frac{AC}{AB}\approx\frac{AC}{500}\approx\frac12\times\frac{BC}{OB}\approx\frac12\times\frac{500}{6370},\]
亦得到上述近似结果.
注: 第一个近似值偏小,而第二个近似计算比第一个近似更接近准确值, 原因为何?
