原题为:
已知椭圆 $C \colon \frac{x^2}{a^2} + \frac{y^2}{b^2} = 1 \,(a > b > 0)$ 的离心率为 $\frac{\sqrt2}2$, 且过点 $A (2, 1)$.
(1) 求 $ C $ 的方程;
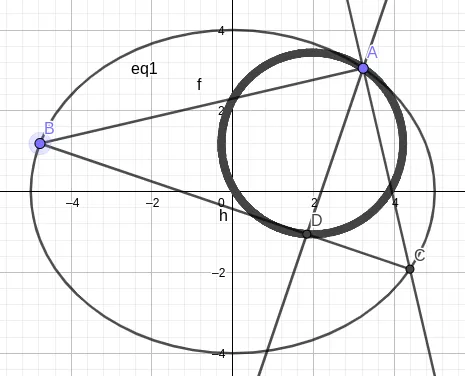
(2) 点 $ M , N $ 在 $ C $ 上, 且 $AM \perp AN $, $AD \perp M N $, $D$ 为垂足. 证明: 存在定 点 $ Q $, 使得 $ |DQ| $ 为定值.
以下探究第二问的一般结论: 若圆锥曲线的离心率 $e \ne \sqrt2$, 则以两条互相垂直于曲线上一定点的弦为直角边构成的直角三角形中, 此定点在斜边上的投影在一定圆上.
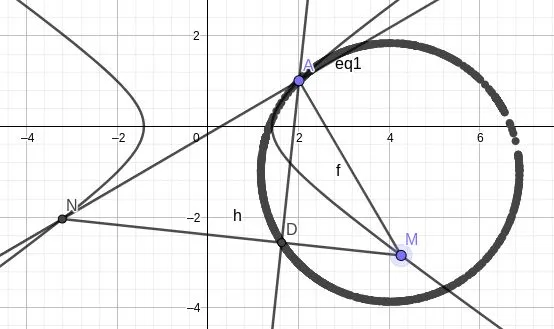
注意到用 $a$ 和 $e$ 表示的椭圆与双曲线方程为同一个表达式, 因而椭圆与双曲线结论统一计算如下.
若 $A(x_0,y_0)$ 且椭圆或双曲线的离心率为 $e$, 设 $M(x_1,y_1)$ 和 $N(x_2,y_2)$.
若 $ MN $ 无斜率, 则其方程即为 $x=x_1$. 根据 $AM \perp AN$ 得
\[ (x_1-x_0,y_1-y_0) \cdot (x_1-x_0,-y_1-y_0)=0, \]
结合 $y^2=(1-e^2)(a^2-x^2)$, 化简得
\[ (2-e^2)x_1^2 – 2x_0x_1 + e^2x_0^2=0, \]
当 $e = \sqrt2$ 时解之得 $x_1 = e^2x_0/2$. 若 $e \ne \sqrt2$ 得 $x_1=\frac{e^2}{2-e^2}x_0$ (舍 $x_1=x_0$).
否则设 $MN \colon y=kx+m$, 与椭圆或双曲线方程联立化简, 得
\[ (k^2+1-e^2)x^2 + 2kmx + m^2-a^2(1-e^2)=0. \]
同理由 $AM \perp AN$ 化简得
\[ (1+k^2)x_1x_2 + (km-ky_0-x_0)(x_1+x_2) + x_0^2 + (m-y_0)^2=0. \]
利用 Vieta 定理, 整理化简得
\[ (2-e^2)m^2 + 2x_0km + x_0^2e^2k^2 – 2(1-e^2)y_0m – e^2y_0^2=0. \]
因式分解之得
\[ (m+x_0k-y_0)((2-e^2)m+e^2x_0k+e^2y_0) = 0, \]
即 $(2-e^2)m+e^2x_0k+e^2y_0 = 0$ (舍 $m+x_0k-y_0=0$, 因 $A \notin MN$).
若 $e = \sqrt2$, 则 $k=-y_0/x_0$, 即此时 $MN$ 为一族平行线, 而 $AD$ 为固定的一条直线 $y_0(y-y_0) = x_0(x-x_0)$.
当 $e \ne \sqrt2$ 时带入 $MN$ 方程化简得
\[ y + \frac{e^2y_0}{2-e^2}= k(x-\frac{e^2x_0}{2-e^2}). \]
设 $P(e^2x_0/(2-e^2),-e^2y_0/(2-e^2))$, 结合 $MN$ 无斜率的情况, 则 $MN$ 恒过 $P$ 点. 根据 $D$ 的定义可知 $D$ 在以 $AP$ 为直径的圆周上, 故取 $Q$ 为 $AP$ 的中点即可.
另外, 容易验证 $x_0y_0 \ne 0$ 时椭圆或双曲线在点 $A$ 处的切线 $\ell$ 斜率为 $k=-x_0(1-e^2)/y_0$, 而 $k_{AP} = y_0/(x_0(1-e^2))$; 而 $x_0y_0 = 0$ 时, $\ell$ 与 $AP$ 的斜率为一零一不存在, 综合得 $\ell \perp AP$.
且 $|AQ| = \sqrt{(1-e^2)(a^2-e^2x_0^2)}/(2-e^2)$, 而 $a^2-e^2x_0^2$ 不就是俩焦半径之积.
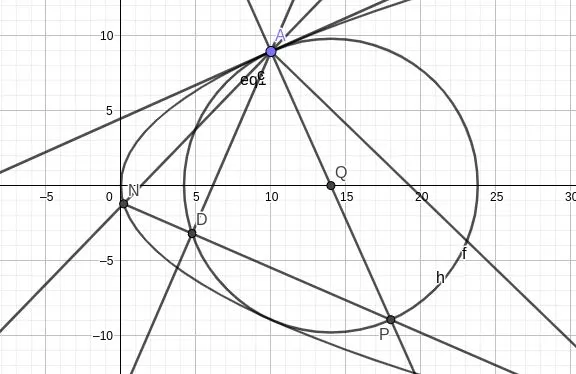
以下探究抛物线的类似结论.
设抛物线方程为 $y^2 = 2px$, $A,M,N$ 分别为 $(y_j^2/(2p),y_j)$, $j=0,1,2$. 设直线 $MN \colon x=hy+m$, 与抛物线方程联立得
\[ y^2-2phy-2pm = 0. \]
由 $AM \perp AN$ 化简得
\[ (y_1y_2 + y_0(y_1+y_2) + y_0^2 + 4p^2)(y_1-y_0)(y_2-y_0) = 0, \]
结合 $M,N$ 的任意性知
\[ y_1y_2 + y_0(y_1+y_2) + y_0^2 + 4p^2 = 0. \]
利用 Vieta 定理可得
\[ -2pm + 2phy_0 + y_0^2 + 4p^2 = 0, \]
即 $m = x_0 + hy_0 + 2p$, 带入直线方程化简即得
\[ x = h(y+y_0) + x_0 + 2p, \]
也就是说 $MN$ 恒过定点 $P(x_0+2p,-y_0)$.
类似地, 根据点 $D$ 的定义可知取 $AP$ 中点为点 $Q(x_0+p,0)$ 即可. 同样可以验证 $AP$ 垂直于抛物线在点 $A$ 处的切线, 另外由点 $Q$ 的特殊性可知, 圆 $Q$ 实际上与抛物线切于点 $A$ 与 $A'(x_0,-y_0)$.
特别地, 若点 $A$ 即为原点, 则点 $P$ 横坐标为 $2p$, 即抛物线中从顶点出发的两条相互垂直的弦另外端点构成的弦与对称轴的交点到顶点的距离为两倍的焦准距.
