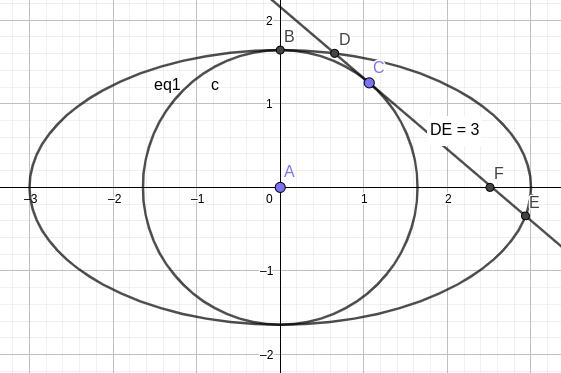
第二问的一般化:
已知椭圆 $E : x^2/a^2 + y^2/b^2 = 1 \, (a>b>0)$ 的离心率 $e \ge \sqrt2/2$, $F$ 为 $E$ 的一个焦点, $M,N$ 为 $E$ 上的两点且直线 $MN$ 与圆 $C : x^2 + y^2 = b^2$ 相切, 则 $F \in MN \iff |MN| = a$.
注:
为了更易看出本质, 只使用半长轴长 $a$ 与离心率 $e$. 则 $E$ 为 $(1-e^2)x^2 + y^2 – a^2(1-e^2) = 0$, $C$ 为 $x^2 + y^2 = a^2(1-e^2)$.
根据对称性, 不妨设 $F(c,0)$. 直线 $MN$ 的倾斜角为 $\alpha$.
证: (1) $F \in MN$, 则 $\sin\alpha = b/c = \sqrt{1-e^2}/e$, 故而 (参考 圆锥曲线过焦点的弦长统一公式)
\[
|MN| = \frac{2a(1-e^2)}{1-e^2\cos^2\alpha} = \frac{2a(1-e^2)}{1-(2e^2-1)} = a.
\]
(2)
$|MN|=a$, 有上述可知只需证明 $\sin\alpha = \sqrt{1-e^2}/e$ 即可. 不妨设 $MN$ 的横截距为 $b/\sin\alpha = a\sqrt{1-e^2}/\sin\alpha$, 则 $MN : x\sin\alpha – y\cos\alpha – a\sqrt{1-e^2} = 0$, 与椭圆方程联立化简得
\[
(1-e^2\cos^2\alpha)x^2 – 2ax\sqrt{1-e^2}\sin\alpha + a^2(1-e^2)\cos^2\alpha = 0,
\]
注意到 $1+\tan^2\alpha = 1/\cos^2\alpha$, 结合 Vieta~定理得
\[
|MN| = \sqrt{(1+\tan^2\alpha)|x_1-x_2|} = \frac{2ae\sqrt{1-e^2}\sin\alpha}{1-e^2\cos^2\alpha},
\]
由已知可得
\[
2e\sqrt{1-e^2}\sin\alpha = 1-e^2\cos^2\alpha = 1-e^2 + e^2\sin^2\alpha,
\]
即 $e\sin\alpha = \sqrt{1-e^2}$, 得证.
